Demystifying Asymptotic Analysis
Asymptotic analysis most of the time begins a data structures and algorithms series and is a very important topic in computer science.
As the size of a program grows, more resources and runtime are needed, and in production, this could lead to scalability issues and hence, the study of data structures and algorithms is necessitated as it helps with runtime and memory size complexity(efficiency).
This improvement can be done by changing data structures to suit a program's needs or writing more efficient algorithms that run faster, and sometimes, it’s a trade-off between runtime and memory efficiency depending on what’s most important in that case being examined.
By definition……
Asymptotic analysis is the evaluation of the runtime of an algorithm mathematically usually with the aim of comparison or improvement.
In calculus class, we learn about asymptotics which is the value for which a function f(x) approaches infinity. The asymptotic analysis uses the size of input as a variable and as the size of input tends to infinity, so does the runtime.
Asymptotic Notations.
There are three main asymptotic notations;
- The Big-O notation (worst-case complexity).
- The Big Theta notation (average-case complexity).
- The Omega notation (best-case complexity).
The Big-O Notation (Landau’s symbol).
The big-O notation which is mathematically expressed as O(n) feeds the maximum runtime of a program under a specified set of inputs in the worst-case scenario. where n represents the length or size of the inputs which is a positive integer constant greater than zero and tends to infinity.
The Big-O notation is the most popular owing to the fact that we often want to criticize and improve our code’s efficiency at runtime.
Expressions of the Big-O notations include;
- Constant time complexity → O(C)
- Linear time complexity → O(n + C)
- Quadratic time complexity → O(n² + n + C)
- Logarithmic time complexity → O(log n)
- Cubic time complexity → O(n³ + …. + C)
Where C represents constants. And the list goes on and on…… and depends on a couple of other factors
The Big Theta Notation.
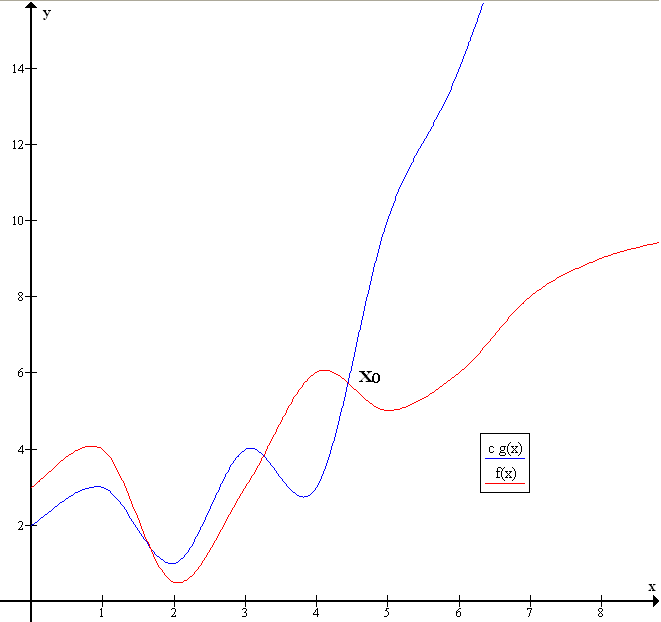
The theta notation is mathematically expressed as θ(n) expresses the lower and upper bounds of an algorithm hence giving the average-time complexity of an algorithm.

From the graph, the runtime is bounded by two functions which represent the best and worst-case complexities, and the runtime is said to be tightly bounded by the functions
The Big Omega Notation.
The big omega notation expressed functionally as Ω(n) gives the upper bounds or best-case complexity of an algorithm at runtime. It feeds us with the minimum time an algorithm will execute for a given set of inputs.

NOTE: is a positive integer from 1 and could tend to infinity for all notations above
Space Complexity (Memory Complexity)
Space complexity has to do with the amount of memory required to run a program. When computer programs are run, memory is allocated to store variables and program execution.
Every language has various data types which have different sizes in memory and earlier, I stated that complexities or time and space depend on the size of the input. For example, the memory required for an array of 100 strings would be greater than that of 30. The end goal is to keep the space complexity at a minimum.
Calculating Space Complexity
The formula for space complexity is given by...
Space Complexity(S(n)) = Auxiliary Space + Input Space
Where the Auxiliary space is the memory used by the algorithms and the Input space is the memory used by inputs such as variables.
Given the following scenarios…..
// Javascript
// CASE 1let a, b, c;
a = b = c = 10;
d = a * b % c
console.log(d)
The integer data type (int 32) takes 4 bytes of data into memory and there are four integer variables a, b, c, d therefore the total space or the space complexity in this instance is 16 and the space complexity is referred to as being a constant one. S(n) = C
// CASE 2spaceFunction = function(){
let a = 2;for(let b = 3; b <= 6; b++){
a += b
}return a
};console.log(spaceFunction())
The function above set the variable a to the integer value, 2 and then runs a loop to add every value from 3 to 6 to the a . The step b <= 6 could vary up to an integer n. Thus, the space complexity is linear, given by O(n).
The Space complexity is calculated as thus…
4 bytes for variables a, b, n which sum up to 12 (The constant term). The Complexity can therefore the expressed as S(n) = n + 12.
Time Complexity
The time complexity of an algorithm is the amount of time it takes the algorithm to run using the number of elementary steps required. Although we could simply use the built-in time module to calculate runtime, it is not as efficient at scale as different computers, depending on the specification run code at varying speeds.
Evaluating Time Complexity of Programs
Evaluating the time complexity of algorithms, we are usually concerned with the time increase as input size increases under the worst-case scenario; so we use the Big-O notation.
Example 1…
//traversing an array JSlet a = [2, 4, 6, 8];for(let b = 0; b < a.length; b++){ // n times c = a[b] // constant time}
To calculate the time complexity T(n), we consider the number of fast-growing terms in the algorithm to note for n, and in this case, the only fast-growing term is the loop variable b , therefore, the algorithm has a linear time complexity O(n) such that the time will only grow as the size of the array grows. The time complexity is given by T(n) = 4n + C (The loop runs 4 times)
Example 2
for(let a = 1; a < 4; a++){ //n timesconsole.log(' ')for(let b = 1; b < 4; b++){ //n timesconsole.log(a * b)
}
}
The program above outputs multiples of a number using a nested loop. There are two loops that run n times and as the size of inputs increase, the run time would increase quadratically. In the above example, T(n) = 16n² + C.
Data Structure Tradeoffs
The data structure used in a program is very important as it could slow down or fasten the time and space complexity of a program. Most developers often choose linked lists over arrays as it is said to be more efficient.
Here’s a brief comparison of both data structures…

Choosing the best data structure for a program increases efficiency and this depends on the operation to be carried out. You can learn more about linked lists here…
This is the end of the time and space for this article, Goodluck on your quest to write efficient code
